
读完这本书,从此爱上数学
很多学生讨厌公式,其实并不是讨厌某这门学科。很多时候,只是抗拒“背诵并应用”的死板考纲要求。
因为教学任务的繁重,不是每一位老师都会向学生挖掘并展示公式之美。这样的欠缺,可以用课外阅读来进行补充。
北京大学出版社出版的《公式之美》,是由量子学派编著,特别邀请43位专家编撰、审核而成的精品佳作。
希望能够带各位读者在数字、字母和符号的碰撞中,感受科学的火花,在简洁、优雅、深邃的公式中,体会科学的震撼之美。
在此之前,除了市面上常见的“公式必背”、“公式大全”,好像还从来没有一本书,以“公式”作为主题进行写作,《公式之美》还为每个公式都创作了一幅插画,这本书因此给很多人带来了耳目一新的感觉。

今天,暂且放下心中对教育制度的愤恨,让我们来一次伟大的数学公式巡礼。
公式“出生”的故事
回想我们的求学阶段,似乎每一个公式都是从石头缝里蹦出来的。正因为如此,这也造成了很多人对于公式的理解和接受产生了困难。
在我们的教育环节,的确忽略了每一个公式都经历过“怀胎孕育”的阶段。认识公式的发明者,了解公式“出生”的故事,并不需要高深的数理知识。
给公式加上温度,便有助于对公式的消化吸收。

我们都知道 1+1=2 ,但你是否想过1+1为什么等于2?
这种终极命题总是显得无聊又深奥,一边觉得莫名其妙,一边又让人头大。
但是,意大利数学家皮亚诺,就用五条公理建立了一阶算术系统,可以用来推导出1+1=2这一最简单的等式。
我们也都知道勾股定理 ,直角三角形中a²+b²=c²。但又是谁孕育出了历史上第一个“数”与“形”结合的公式呢?
提出“勾三股四弦五”的商高错过了“抢注商标”的千古良机,魏晋时期的刘徽以面积关系证明了勾股定理,没想到却还是比古希腊的毕达哥拉斯晚了一步。
更没想到的是,毕达哥拉斯的徒弟希帕索斯,根据勾股定理发现了无理数,竟因触犯教规,被扔进深海里活活淹死,还引发了第一次数学危机。

费马大定理 ,顾名思义,他的孕育者就是数学界的第一“民科”——费马。
费马家境殷实,却天生小气;他口含金钥,却从不挥霍;他生性孤僻,却又希望流芳百世;他自命不凡,又谨小慎微;他热衷挑衅,出了事却只会一味躲避。
正是这样矛盾的性格使得他虽然热爱数学,却依然听从父亲的话考取了公务员。而他也非常任性,提出的定理却从不证明,后世因为他的猜想困扰了358年。
牛顿-莱布尼茨公式 ,这是每一个学过“高数”的人绕不开的名词,也是公式名字中包含的两位科学家反目成仇的缘起。
很多人会用到这个公式,但很少有人知道,牛顿的下半生除了钻研神学、沉迷“点石成金”以外,唯一的爱好就是欺负莱布尼茨……
这些公式背后还有很多富有人情味儿的小故事,这些才是《公式之美》想要读者去了解的。
讲公式,却不只是公式
《公式之美》的目录被分成了两个部分,第一部分是“理论篇”,第二部分是“应用篇”。
◎在“理论篇”中,我们可以看到人类生活的变迁
No.1:万有引力公式
万有引力公式代表的不仅仅是两个物体之间的引力,还代表了人类摆脱了“神力”的束缚,宇宙和万物找到了统一的规律。

No.2:麦克斯韦方程
麦克斯韦不仅预测了电磁波的存在,还启迪了爱迪生等发明家用电取代了蒸汽,人类自此逃离了黑暗。
No.3:质能方程
质能方程宣示了能量和质量之间的转换关系,为人类寻找到了一种“终极能量”,但也打开了潘多拉的魔盒,据联合国统计,全世界核武器的杀伤力相当于人类“自掘坟墓”。
No.4:薛定谔方程
薛定谔方程所描述的粒子,在三维势场中的定态我们或许没有清晰的概念,但很多人都从那只猫的实验中,理解了量子世界的特异功能——量子叠加。
◎在“应用篇”中,我们可以看到现代科技的影子
No.1:香农公式
香农定义了信息传送速率的上限,这么说可能有点太学术,但是问你3G、4G、5G的速度是如何提升的,你可能就要求助香农大神了。
No.2:混沌理论
混沌理论从数学角度诠释了牵一发而动全身的蝴蝶效应,而如今,不管是在天气预报、股票市场、语言研究还是工程技术、生物医药、计算机领域,我们也随处可见混沌理论的身影。
No.3:贝叶斯定理
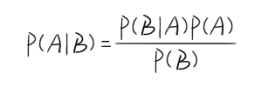
贝叶斯定理不仅仅可以用来求解条件概率,它已经成为了AI工程师的主流算法。公式是客观的,但工程师却可以通过它向AI注射主观基因。未来的人工智能真的会因此学会思考吗?
No.4:椭圆曲线方程
椭圆曲线方程是每一个高考考生都曾经面对的一道题目,但鲜有人知它在比特币中扮演着关键角色,可以说没有椭圆曲线方程,就没有比特币的安全性。
虽然每一个故事都是从一个公式讲起,但我们却从中看到了时代变迁与科技进步。当一个冰冷的公式,与我的生活产生了某种联系,我觉得它似乎也变得更加亲切起来。

公式之美需要发现的眼睛
在自然爱好者眼中,人间最美是高山流水!在人文阅读者眼中,人类至美是诗词歌赋!在爱情至上者眼中,世间最美是化蝶共舞。
而在科学的世界,人间最美的是“天书”般的方程!
大多数时候,我们面对公式的情景都是紧张的学习氛围,甚至没有闲情去欣赏公式本身具有的美。
无理数e,它是自然对数的底,隐藏于飞船的速度和蜗牛的螺线。
无理数π,隐藏于世上最完美的平面对称图形,引爆数字狂热。最简单的两个实数0和1,是构造代数的基础。
“数学界无冕之王”希尔伯特表示,如果在死后500年能重返人间,他最想问:是否已经有人解决了黎曼猜想?过直线外一点,可作其几条平行线?
麦克斯韦的公式融合了电与磁的四大定律,在此之后,电即是磁,磁即是电。

麦克斯韦方程
如果你能看懂这组方程,那么恭喜你,高数基本不会挂掉了;如果你突然虎躯一震,认为只有上帝才能创造如此完美公式,那更恭喜你,你拥有强大的数学审美。
薛定谔方程为好莱坞大片提供了理论基础,骗取了无数票房。迄今为止,量子力学与相对论是关于宇宙彼此不同,又平分秋色的解释。
狄拉克方程预言了反物质(所有已知粒子的镜像)存在。
2017年7月21日,4位华人科学家宣布找到正反同体的“天使粒子”,都不过是在验证1928年伟大的理论物理学家狄拉克(Dirac)作出惊人的预言:宇宙中每一个基本费米粒子必然有相对应的反粒子。
科学家们运用数学思维把奇妙复杂的宇宙规律总结成一道道简洁、完美的公式,便于世人理解和学习。这些公式,对理解世界发展的本质非常重要。尤其是这当下这个大数据时代中,数学逻辑更是一种必修课。
为此,诚荐量子学派《公式之美》,这本书完美呈现了数学的美妙,相信读者读了它定会从此爱上数学,踏入一个崭新的世界。
这本书荣获文津奖科普类图书大奖,是所有科普作品里最专注数学的一本书。既可以自己来读,开拓视野;也可以送给孩子,培养对数学的兴趣。重要的不是记住几个公式,而是爱上数学。
|
